Basis Ortonormal & Gram Schmidt

 NAMA                      : NADYA AURA SALZABILA RAMADHANI

NIM                           : 202231008

KELAS                     : A

PRODI                     : TEKNIK INFORMATIKA

MATKUL                : ALJABAR LINEAR

Ruang Hasil Kali Dalam

Sebuah hasil kali dalam (inner product) pada ruang vektor riil V adalah fungsi yang mengasosiasikan bilangan riil [u,v] dengan masing-masing pasangan vektor u dan v pada v sedemikian rupa sehingga aksioma-aksioma berikut ini :

• [u,v] = [v,u]                                    (aksioma simetri)
• [u+v, w] = [u,w] + [v,w]                (aksioma penambahan)
• [ku, v] = k [u,v]                             (aksioma kehomogenan)
• [u,u] ≥ 0 dan [u,u] = 0  ↔ u = 0   (aksioma kepositifan)

Contoh = 

Jika u = [u1, u2, ... , un], dan v = [v1, v2, ... , vn] adalah vektor vektor pada Rn maka : 

    [u,v] = u • v = u1v1 + u2v2 + ... + unvn 

adalah hasil kali dalam pada ruang Euclides Rn . Dan u dan v dikatakan ortogonal siku [u, v] = 0. Jika u ortogonal terhadap setiap vektor pada V, maka u dikatakan ortogonal terhadap V 

Baris Ortonormal 

Sebuah himpunan vektor pada ruang hasil kali dalam dikatakan ortogonal jika semua pasangan vektor-vektor yang berada dalam himpunan tersebut ortogonal. Sebuah himpunan ortogonal yang setiap vektornya panjangnya 1 disebut ortonormal.

Contoh : 

S =[u1,u2,u3] dengan u1 = [1, 2, 1] , u2 = [1, - 1, 1] , dan u3 = [1, 0, - 1].  Himpunan S adalah ortogonal pada R³  karena [u1,u2]=[u1,u3]=[u2,u3]=0

Catatan: 

Jika S={u1,u2, ... , un}adalah adalah basis ortonormal untuk sebuah ruang hasil kali dalam V, dan jika x sembarang vektor di V, maka :

x= [x, u1] u1 + [x, u2]u2 +...+[x,un ]un

Misalkan V ruang hasil kali dalam dan {u1, u2, ... , u n} himpunan ortonormal jika W ruang yang dibangun oleh u1, u2, ... , un maka setiap vektor x dalam V dapat dinyatakan dengan : x = v + w 

dimana :

v = [v, u1] + [v, u2]u2 + ... + [v, un]un 

Proses Gram-Schmidt 

Setiap ruang hasil kali dalam berdimensi berhingga tak nol, mempunyai sebuah basis ortonormal 

Misalkan S = {u1, u2, ... un} basis untuk ruang hasil kali dalam V, algoritma untuk menentukan ortonormal B = {v1, v2, ... vn} untuk v adalah : 

Langkah 1. Ambil, v₁ = u₁/|u₁|

Langkah 2. Hitung, v₂ , dengan rumus :

 

  

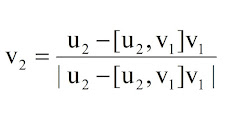
Langkah 3. Hitung, v₃ , dengan rumus :

 

 

Langkah 4. Hitung Vk dengan rumus :

Misalkan S = { u1, u2, u3} basis untuk R³, dengan u1= [1, 0, -1], u2 = [1, 1, -1], dan u3 = [-2, 1, 2]. Carilah basis ortonormal B = {v1, v2,  v3} untuk R³.

Jawab : Langkah 1. Ambil = v1 =  

 

Langkah 2. v2 = x2|x2| dengan x2 = u2 - [u2,v1]v1

 

 

Langkah 3. v3 = x3/|x3|, dengan x3 = u3 - [u3,v1] v1 - [u3,v2] v2