Tugas 4 Determinan Matriks Dan Metode Doolittle
NAMA : NADYA
AURA SALZABILA RAMADHANI
NIM :
202231008
KELAS : A
MATA KULIAH : ALJABAR
LINEAR
PROGRAM STUDI : TEKNIK
INFORMATIKA
A.Sifat – Sifat Determinan
1. Jika A matrik bujur sangkar maka
Det (A) = det (A|)
Contoh :
Menurut sifat (1), maka : det (A) = det (AT) = -36
2. Jika A dan B adalah matrik bujur sangkar berordo sama maka,
Det (AB) = det (A) det (B)
Contoh:
3. Jika A matrik bujur sangkar yang memuat baris atau kolom dimana elemennya 0 atau sebanding, maka
Det (A) = 0
Contoh :
4. Jika A matrik segitiga atas (bawah) yang berordo (nxn) dimana elemen diagonal utama tak nol maka.
Det (A) = a11a22a33…ann
Contoh :
5. Jika A dan B matrik bujur sangkar yang berordo sama. Jika matrik B diperoleh dari A dengan cara mengalikan sembarang baris (kolom) dengan konstanta k tak nol, maka;
Det (B) = k det (A)
Contoh :
6. Jika A dan B matrik bujur sangkar yang berordo sama. Jika matrik B diperoleh dari A dengan cara menukarkan semua elemen sembarang baris (kolom), maka:
Operasi elementarnya adalah :
Bi ß Bj : baris ke – i baru = baris ke – j lama
Ki ß Kj : kolom ke – i baru = kolom ke – j lama
Contoh :
7. Jika A dan B matrik bujur sangkar yang berordo sama. Jika matrik B diperoleh dari A dengan cara mengalihkan sembarang baris (kolom) dengan konstanta k tak nol dan hasilnya dijumlahkan pada baris (kolom) yang lain maka :
Det (B) = det (A)
Operasi elementarnya adalah :
Bi ß Bi + kBj : baris ke–i baru = baris ke–i lama + k baris ke–j lama
Kj ß Kj + k Kj : kolom ke-j bari = kolom ke-j lama + k kolom ke-i lama
Contoh :
B . Teknik Menghitung Invers
a. Teknik Adjoin Matrik
Metode operasi elementer baris metode perkalian invers matrik elementer metode partisi matrik program computer – MATLAB dan WS OFFICE EXCEL
AB = BA = I
“ I “ matrik identitas
· B dikatakan invers matrik A ditulis A-1, maka , AA-1 = A-1A = I
· A dikatakan invers matrik B ditulis B-1, maka, B-1B = BB-1 = I
Contoh :
Contoh :
Untuk kasus n=3
Rumus perhitungannya :
















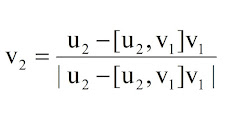
Komentar
Posting Komentar